MondoMisteri MondoMisteri: Il portale dei misteri
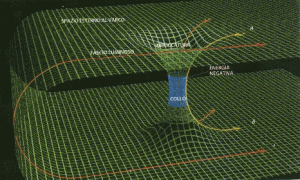
Come limite dell’ergosfera del buco nero di Kerr, l’orizzonte degli eventi di un buco nero rotante è più lontano dal centro del buco all’altezza dell’equatore e non è affatto rigonfio ai poli. Ciò complica la geometria dello spazio-tempo attorno al buco nero di Kerr e contribuisce a spiegare perché i matematici impiegarono così tanto a risolvere le equazioni del caso: la variante di Reissner-Nordstr0m tratta di buchi neri a simmetria sferica (uguali in tutte le direzioni), il che rende, il più delle volte, le equazioni più semplici da risolvere. Una volta che, nel 1963, Kerr scoprì come calcolare gli effetti della rotazione, fu relativamente semplice aggiungere gli effetti della carica elettrica. È ciò che fecero nel 1965, all’Universitàdi Pittsburgh, Ezra Newman e i suoi colleghi; la loro soluzione alle equazioni di Einstein, chiamata soluzione di Kerr-Newman, descrive lo spazio-tempo attorno a un buco nero rotante ed elettricamente carico.
Consideriamo la soluzione di Kerr-Newman: ponendo la carica uguale a zero, si ottiene la descrizione matematica di Kerr di un buco nero rotante; ponendo invece la rotazione uguale a zero ne consegue la soluzione di Reissner-Nordstr0m per un buco nero carico; se si pongono sia la carica che la rotazione uguali a zero si ottiene la soluzione di Schwarzchild per un buco nero non rotante e senza carica. La soluzione di Kerr-Newman delle equazioni di Einstein comprende tutte le proprietà che può avere un buco nero: massa, carica e rotazione. In accordo con il teorema “senza peli”, è questa la soluzione finale delle equazioni, almeno per quanto riguarda i buchi neri. Ma poiché non c’è alcuna ragione per pensare che buchi neri in rotazione o senza rotazione abbiano realmente carica, non aggiungerò nient’altro riguardo alla soluzione di Kerr-Newman e concentrerò la mia attenzione sulle interessanti pos sibilità offerte dalla sola aggiunta della rotazione a un buco nero massivo. Innanzitutto consideriamo la singolarità anulare; supponiamo che essa sia sufficientemente ampia e che il buco nero sia abbastanza massivo perché l’astronauta non venga fatto a pezzi da forze di marea.
È in questo caso possibile entrare in un buco nero di Kerr lungo uno dei suoi poli e attraversare l’anello formato dalla singolarità! Se ciò si facesse realmente, si entrerebbe in un mondo “capovolto”. Le equazioni ci dicono che non appena oltrepassato l’anello, si penetra in una regione dello spazio-tempo in cui il prodotto della distanza dal centro dell’anello stesso per la forza di gravità è negativo. Questo potrebbe significare che la gravità si comporta in modo perfettamente normale, ma che si è arrivati in una regione di spazio negativo, in cui è possibile, ad esempio, misurare “-10 km” dal centro del buco. Gli stessi relativisti non accettano di buon grado questa possibilità e quindi interpretano di solito il risultato negativo come una inversione della gravità; passando attraverso l’anello la forza gravitazionale attrattiva si trasformerebbe in forza repulsiva. In questa regione dello spazio-tempo, il buco nero è dotato di una gravità che allontana da sé sia la materia che la luce; esso si comporta come un buco bianco, di cui abbiamo già parlato.
Non è affatto semplice accogliere questa teoria; tra l’altro le equazioni che descrivono l’universo ad antigravità hanno conseguenze ancora più estreme. Un astronauta che penetri attraverso l’anello e che rimanga poi nei suoi pressi, girando attorno al centro del buco nero in una orbita opportuna viaggerebbe indietro nel tempo. Nella fisica convenzionale ci si salva in extremis sostenendo che pur così facendo – ripassando attraverso l’anello per uscire dal buco nero in rotazione – non si potrebbe tuttavia tornare indietro nella stessa regione di spazio-tempo da cui si è partiti. Analogamente all’orizzonte degli eventi del buco nero di ReissnerNordstr0m, l’orizzonte del buco nero di Kerr permette viaggi di sola andata e conduce in un altro universo. In un certo senso si potrebbe arrivare “prima” di essere partiti dall’universo originario, ma non esisterebbe di fatto alcun sistema per comunicare con il luogo di partenza, ovvero per poter trasmettere a se stessi un messaggio prima di iniziare il viaggio.
Ciò nonostante, come si può immaginare un buco nero dotato di carica così forte da far sì che l’orizzonte degli eventi interno si accresca e sorpassi l’orizzonte esterno, lasciando esposta la singolarità in esso contenuta, così un buco nero di Kerr che ruoti con sufficiente rapidità distruggerà i suoi orizzonti degli eventi, lasciando visibile la singolarità nuda. Ma questa singolarità, al contrario di quella del buco nero di Reissner-Nordstr0m, manterrà la sua forma ad anello. Non solo sarebbe possibile viaggiarci attraverso, ma anche guardarci dentro da lontano, per mezzo di potenti telescopi. E se si attraversasse l’anello sbucando nella regione a tempo negativo, non esisterebbero più orizzonti a una sola via che potrebbero impedire di ritornare da dove si è partiti. Il diagramma di Penrose che rappresenta que,sta situazione è molto semplice. Esso consiste di un universo negativo e di uno positivo, separati da una singolarità anulare attraverso cui può passare qualunque corpo, che quindi può viaggiare da un universo all’altro. Teoricamente sarebbe possibile avvicinarsi alla singolarità da un punto qualunque dello spazio e del tempo di uno dei due universi, orbitare in modo opportuno attorno alla singolarità e ritornare esattamente nello stesso luogo da cui si è partiti, ma in un momento nel tempo anteriore alla partenza.
Se esiste questa singolarità nuda di Kerr in qualche parte dell’Universo, allora per voi è teoricamente possibile, se solo riusciste a scoprire il percorso giusto, partire da dove siete seduti ora e andare in un luogo qualunque dell’Universo in un’epoca qualsiasi da voi scelta (passata, presente o futura). Anche in questo caso non sarebbe necessario viaggiare più veloci della luce. Naturalmente durante il viaggio si potrebbe morire di vecchiaia, ma non è questo che ci interessa. Le equazioni della relatività generale, la migliore descrizione dello spazio-tempo disponibile, permettono esplicitamente di viaggiare nel tempo. Non bisogna stupirsi se la maggior parte dei fisici invoca disperatamente la legge della censura cosmica e si preoccupa moltissimo del fatto che non esista nessuna prova che dimostri che la natura obbedisca ad essa; ma almeno essi si possono consolare con il fatto che sarebbe estremamente difficile far motare un buco nero abbastanza rapidamente da far sì che il suo momento angolare dissolva l’orizzonte degli eventi. Singolarità nude di questo genere sarebbero soluzioni inattuabili delle equazioni di Einstein, anche se, in senso stretto, non sono impossibili. Lasciamo ora da parte le bizzarre proprietà della singolarità anulare ed esaminiamo di nuovo la mappa spazio-temporale di un buco nero di Kerr..
A parte questo “ammorbidimento” della singolarità che permette al viaggiatore di attraversare l’anello e di tornare indietro, la mappa spazio-temporale della geometria di Kerr è proprio come la topologia delle bambole di carta della geometria di Reissner-Nordstr0m. Trascurando la regione a tempo negativo nella quale la “morbidezza” della singolarità è visualizzata con gli spazi tra i denti della linea a dente di sega, generalmente usata per indicare la linea di universo di una singolarità. In fin dei conti sembrerebbe che questi buchi neri rotanti fornissero connessioni iperspaziali con altre regioni dello spazio-tempo (ovvero altri universi). Negli anni ’70, tuttavia, nuovi calcoli suggerirono che nell’Universo reale potenti effetti gravitazionali associati alle singolarità e agli orizzonti degli eventi avrebbero troncato queste connessioni iperspaziali prima che qualsiasi cosa le potesse attraversare: sembrava che i cunicoli sarebbero potuti esistere solo in un universo vuoto.
L’ostacolo dello spostamento verso il blu
Il problema dei cunicoli che ho appena presentato venne posto per la prima volta dai matematici che indagavano la natura dei buchi bianchi. Un matematico in particolare, Douglas Eardley, del CalTech, all’inizio degli anni ’70 sembrava che avesse dimostrato definitivamente che i buchi bianchi non possono esistere nell’universo reale. Per me era una notizia particolarmente spiacevole, perché minava le fondamenta di una spiegazione piuttosto soddisfacente sulla formazione delle galassie, una teoria sviluppata da ricercatori sovietici negli anni ’60, a cui io ero particolarmente affezionato, e su cui avevo anche scritto un libro. L’esponente principale della rinascita dell’idea dei buchi bianchi fu, negli anni ’60, Igor Novikov, il quale si interessava alle enormi esplosioni di attività dell’Universo, come il caso dei quasar. A quel tempo nessuno aveva calcolato come la materia in caduta in un buco nero supermassivo potesse generare energia a sua volta riespulsa lungo le regioni polari. Quindi è naturale che alcuni ricercatori si chiedessero se i buchi bianchi non potessero spiegare più adeguatamente questo fenomeno di quanto non facessero i buchi neri.
Novikov propose che la singolarità primordiale, anziché esplodere in un unico Big Bang, avesse delle parti che ritardavano in qualche modo la loro espansione, esplodendo nell’Universo in data successiva. Questi “nuclei ritardati” (Jogging Gores) avrebbero allora riversato materia nell’Universo proprio come fanno i quasar. Inoltre la gravità di un nucleo lento, ancor prima di esplodere, avrebbe potuto trattenere una nube di materia nell’Universo in espansione; se in questa nube si fossero formate delle stelle, si sarebbe potuta spiegare l’origine delle galassie.
Queste, ahimé, erano tutte quelle idee che l’opera di Eardley minò. Iniziamo a vedere il perché esaminando altri dia grammi di Penrose. Oltre ai buchi neri e ai buchi bianchi, i relativisti parlano talvolta di “buchi grigi”. Un buco nero è un oggetto in cui precipitano materia e radiazioni, ma da cui nulla fuoriesce. Un buco bianco è un oggetto da cui fuoriescono materia e radiazioni, ma in cui nulla precipita. Un buco grigio è un oggetto che emette materia e radiazioni le quali, dopo aver raggiunto una certa distanza dall’orizzonte degli eventi, ricadono nel bucol. In ogni caso ricordate che il buco nero, bianco o grigio è descritto da due singolarità, una passata e l’altra futura.
Lo spazio-tempo è descritto accuratamente dalla soluzione di Schwarzchild delle equazioni di Einstein solo nella regione esterna alla superficie della stella. La stella stessa impedisce che una parte considerevole del diagramma abbia un significato reale. La metrica di Schwarzchild entra in gioco solo quando la stella collassa; però può esistere realmente solo la singolarità futura. Per una stella realistica in collasso non esiste nessun orizzonte degli eventi o singolarità passati da cui possa emergere un oggetto qualunque. Delle tre varianti matematicamente possibili, solo il buco nero è una prospettiva realistica da un punto di vista fisico. Naturalmente se la stella in collasso ruota con velocità sufficiente, si ha ancora la possibilità che si crei un buco nero di Kerr che metta in comunicazione con qualche altro universo, dove la materia che collassa nel buco nero del nostro universo potrebbe riemergere come buco bianco da un orizzonte degli eventi passato; ma anche accettando questo scenario si presentano diversi problemi.
Il primo problema riguarda la radiazione di Hawking. Singolarità che giacciono orizzontalmente nel diagramma spazio-temporale del futuro (definite di “tipo spaziale” in quanto occupano tutto lo spazio, ma solo un momento nel tempo) non subiscono le conseguenze dell’evaporazione di Hawking. Dal punto di vista di una singolarità di questo tipo, tutto il tempo si trova nel passato, e non esiste futuro in cui l’evaporazione di Hawking possa verificarsi (supponendo sempre che il flusso del tempo non possa essere invertito, questione ancora discussa). Una singolarità passata di tipo spaziale, d’altra parte, può produrre una moltitudine di particelle grazie al processo di Hawking, e forse può addirittura evaporare nel nulla assoluto. Il destino di queste particelle è, naturalmente, quello di colmare il buco nero e di precipitare inevitabilmente nello stesso punto, formando una singolarità futura di tipo spaziale. Ciò non cambia poi di molto la rappresentazione di un buco nero di Schwarzchild, anche se getta nuova luce su quello che puo’ accadere all’interno del buco, dove si pensava non avvenisse nulla di interessante. Il problema nasce quando applichiamo lo stesso ragionamento alla singolarità “verticale” (o di “tipo temporale”) associata a buchi neri carichi in rotazione.
Dopo tutto è la rotazione di 90° – che trasforma la singolarità futura in una singolarità di tipo temporale – che, teoricamente, rende possibile a un’astronave di passare attraverso un buco nero e di raggiungere un altro universo senza essere distrutta dalla gravità. Ma se questa singolarità di tipo spaziale evapora con il processo di Hawking, cosa accade alle particelle prodotte? Secondo quella che alcuni fisici ritengono sia la più semplice interpretazione delle equazioni, le particelle devono di nuovo colmare il buco nero e accumularsi in un momento nel futuro, formando una singolarità futura di tipo spaziale e aprendo la strada verso nuovi universi. Devo confessare che queste argomentazioni non mi convincono pienamente. È un punto chiave dell’evaporazione di Hawking, nella sua versione originale, che ci siano dei processi all’orizzonte degli eventi tali che, se tin membro di una coppia di particelle prodotte riesce a fuggire, il partner cade nel buco in uno stato di energia negativa. Non è affatto scontato che lo stesso tipo di processo avvenga oltre l’orizzonte degli eventi, in prossimità di ciò che equivale a una singolarità nuda. Eppure matematici più eminenti di quanto io non sia sembrano considerare seriamente questa idea; se hanno ragione, allora parrebbe che i fenomeni quantistici chiudano la porta di accesso ad altri mondi che era stata aperta dalla relatività generale.
Ma poiché non disponiamo ancora di una teoria completa che combini in un unico gruppo di equazioni la fisica dei quanti e la relatività generale, questa spiacevole conclusione non può essere considerata l’ultima parola sull’argomento. Si può notare quanto sia semplice capovolgere i risultati sui buchi neri osservando quello che è accaduto alle ricerche di Eardley, le quali, al tempo in cui vennero presentate, sembravano negare definitivamente l’esistenza dei buchi bianchi unicamente sulla base della relatività generale. Il punto importante messo in luce da Eardley, grazie alla sua visione più realistica del collasso di una stella in un buco nero, è che si deve tener conto della distribuzione reale di materia nell’Universo esterno e non solo delle eleganti equazioni che descrivono lo spazio-tempo curvo. Questo problema non si pone quando si deve descrivere il Big Bang, poiché al tempo della creazione non esisteva lo spazio e dunque non ci si doveva preoccupare della materia e dell’energia esterne. Ma per un nucleo ritardato la situazione è differente.
Ho già detto che una delle caratteristiche affascinanti dell’idea di Novikov era che la gravità di un nucleo ritardato trattenesse materia, spiegando così la presenza delle galassie nell’Universo in espansione; la difficoltà della teoria è che il nucleo ritardato tratterrebbe in modo troppo efficiente la materia e la luce. Ricordate che la lu ce che abbandona la superficie di un buco nero viene spostata verso il rosso tanto da perdere tutta la sua energia: lo spostamento verso il rosso è infinito. Ma la luce che cade in un buco nero guadagna energia, e quando attraversa l’orizzonte degli eventi viene spostata infinitamente verso il blu. Questo non ci interessa finché l’energia accumulata rimane tranquillamente chiusa nel buco nero stesso. Ora pensiamo invece che cosa accadrebbe a un buco bianco qualora tentasse di emergere da una singolarità in un universo reale che già contiene materia ed energia.
Il nucleo in espansione di un buco bianco possiederà in ogni suo punto un campo gravitazionale potente quanto il buco nero equivalente. Quindi la materia e l’energia dell’Universo esterno inizieranno ad accumularsi sulla superficie dell’oggetto, sebbene il buco bianco al suo interno cerchi di espandersi. Il problema è particolarmente grave per tutti i nuclei ritardati rimasti dal Big Bang, poiché nella palla infuocata della creazione essi sarebbero stati circondati da un vortice ribollente di energia di cui si potevano alimentare; ma Eardley dimostrò che persino nell’Universo attuale è disponibile energia più che sufficiente – persino solo come luce stellare – da permettere una sua accumulazione nell’orizzonte degli eventi. Dopotutto, se lo spostamento verso il blu è infinito, una minima quantità di luce che precipiti nel buco bianco basta a crearci difficoltà. Questi problemi si concretizzano in quella che oggi viene chiamata parete blu (blue sheet), un muro di energia che circonda il buco bianco così intenso che la stessa energia della luce ripiega lo spazio-tempo tanto da creare un buco nero intorno al buco bianco iniziale.
Il fisico di Stanford Nick Herbert ha reso icasticamente questo fenomeno: “Universi come il nostro contengono quantità letali di luçe e di materia, che formano pareti blu fatali che soffocano buchi bianchi ancora in fasce”. Più prosaicamente si può dire che i calcoli dimostrano che il processo di soffocamento richiederebbe circa un millesimo di secondo qualora i nuclei ritardati dell’universo odierno decidessero di accelerare e cercassero di diventare buchi bianchi. O, ancor peggio, il processo di soffocamento potrebbe “trasformare” la soluzione di Schwarzchild in quella di Reissner-Nordstf0m o in quella di Kerr. Naturalmente buchi di questo genere hanno sempre orizzonti degli eventi passati. L’accumulazione di energia all’orizzonte degli eventi passato inizia nel momento in cui viene creato l’Universo (e l’orizzonte) e forma una parete blu impenetrabile.
Nessuno ha ancora risolto del tutto il difficile problema matematico della descrizione esatta dell’interazione tra questa parete blu e il cunicolo, ma alla fine degli anni ’80 la maggior parte dei fisici considerava probabile l’esistenza di pareti blu che troncavano la connessione tra universi. Immaginate allora la loro sorpresa, quando i calcoli condotti al termine delgli anni ’80 e all’inizio degli anni ’90 dimostrarono che ciò, in fin dei conti, poteva anche non avvenire.
La divisione della parete blu
Questa dimostrazione venne eseguita da Thorne e dai suoi colleghi, che avevano iniziato le ricerche sui cunicoli attraversabili perché stimolati dalle richieste di Sagan. Essa è una conseguenza logica dello studio di Eardley sulle pareti blu, cosicché è meglio discuterne subito, prima (lo prometto!) di tornare a situazioni fantascientifiche e alle reali novità che ne derivano. Eardley dimostrò che nell’Universo reale sorgono problemi con le pareti blu perché, oltre a considerare la curvatura dello spazio-tempo attorno alle singolarità, bisogna tener presente il modo in cui lo spazio-tempo curvo interagisce con la materia e con l’energia dell’Universo esterno. Ma come si verifica questa interazione? I calcoli presupponevano che lo spazio-tempo esterno al buco bianco/nero fosse piatto.
Ciò è tanto prossimo al vero – per estensioni di spazio sulla scala del sistema solare o della nostra Galassia – che gli esperti lo considerano praticamente sicuro; ma sulla scala di tutto l’Universo lo spazio-tempo potrebbe anche non essere piatto. Le equazioni cosmo logiche di Einstein, che ci dicono che l’Universo è in contrazione o in espansione, ci suggeriscono anche come sia molto improbabile una geometria del cosmo piatta: essa dovrebbe essere non euclidea e curva (aperta, come la superficie a sella , o chiusa, come la superficie di una sfera). I ricercatori dell’Università di Newcastle upon Tyne hanno dimostrato che, se l’Universo è effettivamente chiuso ( è questa l’ipotesi attualmente preferita da molti cosmologi, per molte ragioni esposte analiticamente in Cosmic Coincidences, , ci potrebbero essere dopotutto dei punti deboli nella teoria delle pareti blu, se non nelle pareti blu stesse.
